確率キュー位置モデル
概要
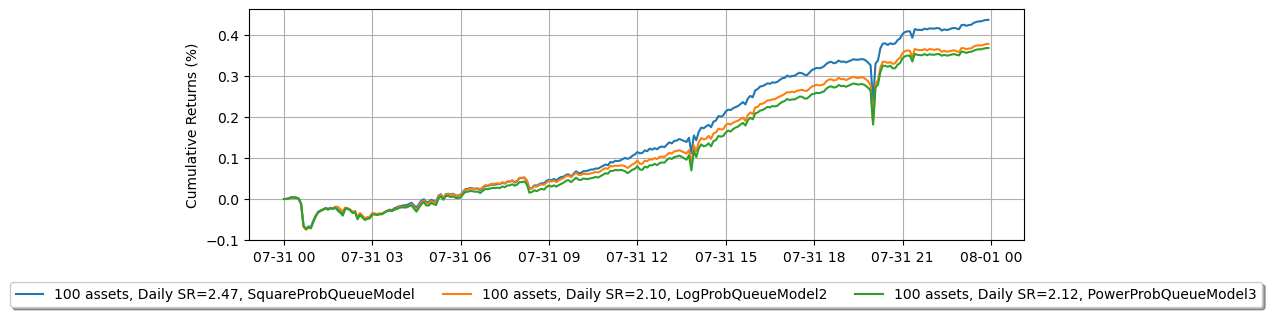
ここでは、キュー位置モデルが注文の充足シミュレーションにどのように影響し、最終的に戦略のパフォーマンスにどのように影響するかを示します。正確なバックテストを行うためには、バックテストと実際の取引結果を比較して適切なキュー位置モデルを見つけることが重要です。この文脈では、キュー位置モデルを変更することで比較を示します。これにより、バックテストと実際の取引結果が一致する適切なキュー位置モデルを特定できます。
注: この例は教育目的のみであり、高頻度マーケットメイキングスキームの効果的な戦略を示しています。すべてのバックテストは、Binance Futuresで利用可能な最高のマーケットメイカーリベートである0.005%のリベートに基づいています。詳細については、Binance Upgrades USDⓢ-Margined Futures Liquidity Provider Program を参照してください。
[1]:
import numpy as np
from numba import njit, uint64
from numba.typed import Dict
from hftbacktest import (
BacktestAsset,
ROIVectorMarketDepthBacktest,
GTX,
LIMIT,
BUY,
SELL,
BUY_EVENT,
SELL_EVENT,
Recorder
)
from hftbacktest.stats import LinearAssetRecord
@njit(cache=True)
def measure_trading_intensity(order_arrival_depth, out):
max_tick = 0
for depth in order_arrival_depth:
if not np.isfinite(depth):
continue
# Sets the tick index to 0 for the nearest possible best price
# as the order arrival depth in ticks is measured from the mid-price
tick = round(depth / .5) - 1
# In a fast-moving market, buy trades can occur below the mid-price (and vice versa for sell trades)
# since the mid-price is measured in a previous time-step;
# however, to simplify the problem, we will exclude those cases.
if tick < 0 or tick >= len(out):
continue
# All of our possible quotes within the order arrival depth,
# excluding those at the same price, are considered executed.
out[:tick] += 1
max_tick = max(max_tick, tick)
return out[:max_tick]
@njit(cache=True)
def linear_regression(x, y):
sx = np.sum(x)
sy = np.sum(y)
sx2 = np.sum(x ** 2)
sxy = np.sum(x * y)
w = len(x)
slope = (w * sxy - sx * sy) / (w * sx2 - sx**2)
intercept = (sy - slope * sx) / w
return slope, intercept
@njit(cache=True)
def compute_coeff_simplified(gamma, delta, A, k):
inv_k = np.divide(1, k)
c1 = inv_k
c2 = np.sqrt(np.divide(gamma * np.exp(1), 2 * A * delta * k))
return c1, c2
@njit
def gridtrading_glft_mm(hbt, recorder, gamma, order_qty):
asset_no = 0
tick_size = hbt.depth(asset_no).tick_size
arrival_depth = np.full(30_000_000, np.nan, np.float64)
mid_price_chg = np.full(30_000_000, np.nan, np.float64)
t = 0
prev_mid_price_tick = np.nan
mid_price_tick = np.nan
tmp = np.zeros(500, np.float64)
ticks = np.arange(len(tmp)) + 0.5
A = np.nan
k = np.nan
volatility = np.nan
delta = 1
grid_num = 20
max_position = 50 * order_qty
# Checks every 100 milliseconds.
while hbt.elapse(100_000_000) == 0:
#--------------------------------------------------------
# Records market order's arrival depth from the mid-price.
if not np.isnan(mid_price_tick):
depth = -np.inf
for last_trade in hbt.last_trades(asset_no):
trade_price_tick = last_trade.px / tick_size
if last_trade.ev & BUY_EVENT == BUY_EVENT:
depth = max(trade_price_tick - mid_price_tick, depth)
else:
depth = max(mid_price_tick - trade_price_tick, depth)
arrival_depth[t] = depth
hbt.clear_last_trades(asset_no)
hbt.clear_inactive_orders(asset_no)
depth = hbt.depth(asset_no)
position = hbt.position(asset_no)
orders = hbt.orders(asset_no)
best_bid_tick = depth.best_bid_tick
best_ask_tick = depth.best_ask_tick
prev_mid_price_tick = mid_price_tick
mid_price_tick = (best_bid_tick + best_ask_tick) / 2.0
# Records the mid-price change for volatility calculation.
mid_price_chg[t] = mid_price_tick - prev_mid_price_tick
#--------------------------------------------------------
# Calibrates A, k and calculates the market volatility.
# Updates A, k, and the volatility every 5-sec.
if t % 50 == 0:
# Window size is 10-minute.
if t >= 6_000 - 1:
# Calibrates A, k
tmp[:] = 0
lambda_ = measure_trading_intensity(arrival_depth[t + 1 - 6_000:t + 1], tmp)
if len(lambda_) > 2:
lambda_ = lambda_[:70] / 600
x = ticks[:len(lambda_)]
y = np.log(lambda_)
k_, logA = linear_regression(x, y)
A = np.exp(logA)
k = -k_
# Updates the volatility.
volatility = np.nanstd(mid_price_chg[t + 1 - 6_000:t + 1]) * np.sqrt(10)
#--------------------------------------------------------
# Computes bid price and ask price.
c1, c2 = compute_coeff_simplified(gamma, delta, A, k)
half_spread_tick = c1 + delta / 2 * c2 * volatility
skew = c2 * volatility
normalized_position = position / order_qty
reservation_price_tick = mid_price_tick - skew * normalized_position
bid_price_tick = min(np.round(reservation_price_tick - half_spread_tick), best_bid_tick)
ask_price_tick = max(np.round(reservation_price_tick + half_spread_tick), best_ask_tick)
bid_price = bid_price_tick * tick_size
ask_price = ask_price_tick * tick_size
grid_interval = max(np.round(half_spread_tick) * tick_size, tick_size)
bid_price = np.floor(bid_price / grid_interval) * grid_interval
ask_price = np.ceil(ask_price / grid_interval) * grid_interval
#--------------------------------------------------------
# Updates quotes.
# Creates a new grid for buy orders.
new_bid_orders = Dict.empty(np.uint64, np.float64)
if position < max_position and np.isfinite(bid_price):
for i in range(grid_num):
bid_price_tick = round(bid_price / tick_size)
# order price in tick is used as order id.
new_bid_orders[uint64(bid_price_tick)] = bid_price
bid_price -= grid_interval
# Creates a new grid for sell orders.
new_ask_orders = Dict.empty(np.uint64, np.float64)
if position > -max_position and np.isfinite(ask_price):
for i in range(grid_num):
ask_price_tick = round(ask_price / tick_size)
# order price in tick is used as order id.
new_ask_orders[uint64(ask_price_tick)] = ask_price
ask_price += grid_interval
order_values = orders.values();
while order_values.has_next():
order = order_values.get()
# Cancels if a working order is not in the new grid.
if order.cancellable:
if (
(order.side == BUY and order.order_id not in new_bid_orders)
or (order.side == SELL and order.order_id not in new_ask_orders)
):
hbt.cancel(asset_no, order.order_id, False)
for order_id, order_price in new_bid_orders.items():
# Posts a new buy order if there is no working order at the price on the new grid.
if order_id not in orders:
hbt.submit_buy_order(asset_no, order_id, order_price, order_qty, GTX, LIMIT, False)
for order_id, order_price in new_ask_orders.items():
# Posts a new sell order if there is no working order at the price on the new grid.
if order_id not in orders:
hbt.submit_sell_order(asset_no, order_id, order_price, order_qty, GTX, LIMIT, False)
#--------------------------------------------------------
# Records variables and stats for analysis.
t += 1
if t >= len(arrival_depth) or t >= len(mid_price_chg):
raise Exception
# Records the current state for stat calculation.
recorder.record(hbt)
[2]:
def backtest(args):
asset_name, asset_info, model = args
# Obtains the mid-price of the assset to determine the order quantity.
snapshot = np.load('data/{}_20230730_eod.npz'.format(asset_name))['data']
best_bid = max(snapshot[snapshot['ev'] & BUY_EVENT == BUY_EVENT]['px'])
best_ask = min(snapshot[snapshot['ev'] & SELL_EVENT == SELL_EVENT]['px'])
mid_price = (best_bid + best_ask) / 2.0
latency_data = np.concatenate(
[np.load('latency/live_order_latency_{}.npz'.format(date))['data'] for date in range(20230731, 20230732)]
)
asset = (
BacktestAsset()
.data(['data/{}_{}.npz'.format(asset_name, date) for date in range(20230731, 20230732)])
.initial_snapshot('data/{}_20230730_eod.npz'.format(asset_name))
.linear_asset(1.0)
.intp_order_latency(latency_data)
.no_partial_fill_exchange()
.trading_value_fee_model(-0.00005, 0.0007)
.tick_size(asset_info['tick_size'])
.lot_size(asset_info['lot_size'])
.roi_lb(0.0)
.roi_ub(mid_price * 5)
.last_trades_capacity(10000)
)
if model == 'SquareProbQueueModel':
asset.power_prob_queue_model(2)
elif model == 'LogProbQueueModel2':
asset.log_prob_queue_model2()
elif model == 'PowerProbQueueModel3':
asset.power_prob_queue_model3(3)
else:
raise ValueError
hbt = ROIVectorMarketDepthBacktest([asset])
# Sets the order quantity to be equivalent to a notional value of $100.
order_qty = max(round((100 / mid_price) / asset_info['lot_size']), 1) * asset_info['lot_size']
recorder = Recorder(1, 30_000_000)
gamma = 0.00005
gridtrading_glft_mm(hbt, recorder.recorder, gamma, order_qty)
hbt.close()
recorder.to_npz('stats/gridtrading_simple_glft_qm_{}_{}.npz'.format(model, asset_name))
[3]:
%%capture
from multiprocessing import Pool
import json
with open('assets2.json', 'r') as f:
assets = json.load(f)
with Pool(16) as p:
print(p.map(backtest, [(k, v, 'SquareProbQueueModel') for k, v in assets.items()]))
with Pool(16) as p:
print(p.map(backtest, [(k, v, 'LogProbQueueModel2') for k, v in assets.items()]))
with Pool(16) as p:
print(p.map(backtest, [(k, v, 'PowerProbQueueModel3') for k, v in assets.items()]))
[4]:
import polars as pl
from matplotlib import pyplot as plt
def compute_net_equity(model):
equity_values = {}
sr_values = {}
for asset_name in assets.keys():
data = np.load('stats/gridtrading_simple_glft_qm_{}_{}.npz'.format(model, asset_name))['0']
stats = (
LinearAssetRecord(data)
.resample('5m')
.stats()
)
equity = stats.entire.with_columns(
(pl.col('equity_wo_fee') - pl.col('fee')).alias('equity')
).select(['timestamp', 'equity'])
pnl = equity['equity'].diff()
sr = np.divide(pnl.mean(), pnl.std())
equity_values[asset_name] = equity
sr_values[asset_name] = sr
sr_m = np.nanmean(list(sr_values.values()))
sr_s = np.nanstd(list(sr_values.values()))
asset_number = 0
net_equity = None
for i, (equity, sr) in enumerate(zip(equity_values.values(), sr_values.values())):
# There are some assets that aren't working within this scheme.
# This might be because the order arrivals don't follow a Poisson distribution that this model assumes.
# As a result, it filters out assets whose SR falls outside -0.5 sigma.
if (sr - sr_m) / sr_s > -0.5:
asset_number += 1
if net_equity is None:
net_equity = equity.clone()
else:
net_equity = net_equity.select(
'timestamp',
(pl.col('equity') + equity['equity']).alias('equity')
)
if asset_number == 100:
# 5_000 is capital for each trading asset.
return net_equity.with_columns(
(pl.col('equity') / asset_number / 5_000).alias('equity')
)
np.seterr(divide='ignore', invalid='ignore')
fig = plt.figure()
fig.set_size_inches(10, 3)
legend = []
for model in ['SquareProbQueueModel', 'LogProbQueueModel2', 'PowerProbQueueModel3']:
net_equity_ = compute_net_equity(model)
pnl = net_equity_['equity'].diff()
# Since the P&L is resampled at a 5-minute interval
sr = pnl.mean() / pnl.std() * np.sqrt(24 * 60 / 5)
legend.append('100 assets, Daily SR={:.2f}, {}'.format(sr, model))
plt.plot(net_equity_['timestamp'], net_equity_['equity'] * 100)
plt.legend(
legend,
loc='upper center', bbox_to_anchor=(0.5, -0.15),
fancybox=True, shadow=True, ncol=3
)
plt.grid()
plt.ylabel('Cumulative Returns (%)')
[4]:
Text(0, 0.5, 'Cumulative Returns (%)')